Lectures: topics and speakers

Asymptotic symmetries from a geometric point of view    by Luca CIAMBELLI (ULB, Brussels).

This lecture consists of three main parts. The first is devoted to Noether theorems and their underlying framework, the covariant phase space, with special focus on gauge theories. Surface charges are introduced and their algebra is shown to projectively represent the asymptotic symmetry algebra. Integrability and conservation of charges are addressed. In the second part, we introduce the universal corner symmetry and enunciate the corner proposal. The last part of this lecture is about the extended phase space, and, time permitting, scattered recent advancements in the understanding of gauge symmetries. Various exercises are proposed, to accompany and elucidate the arguments exposed.

Noncommutative Geometry with applications to physics    by Arkadiusz BOCHNIAK (Jagiellonian University, Kraków).

TBA

De Sitter space & holography    by Damian GALANTE (King's College London).

TBA

Geometric Quantization    by Konstantin WERNLI (University of Southern Denmark, Odense).

Geometric Quantization is a mathematical way of trying to satisfy Dirac’s axioms for quantization. It is formulated in the language of phase spaces or symplectic geometry. One of its main advantages is the possibility to quantize a large class of symplectic manifolds. I will give a pedestrian introduction to the subject, with the goal of discussing some applications to (topological) quantum field theory.

Introduction to higher-spin theories    by Simon PEKAR (UMONS, Mons).

TBA

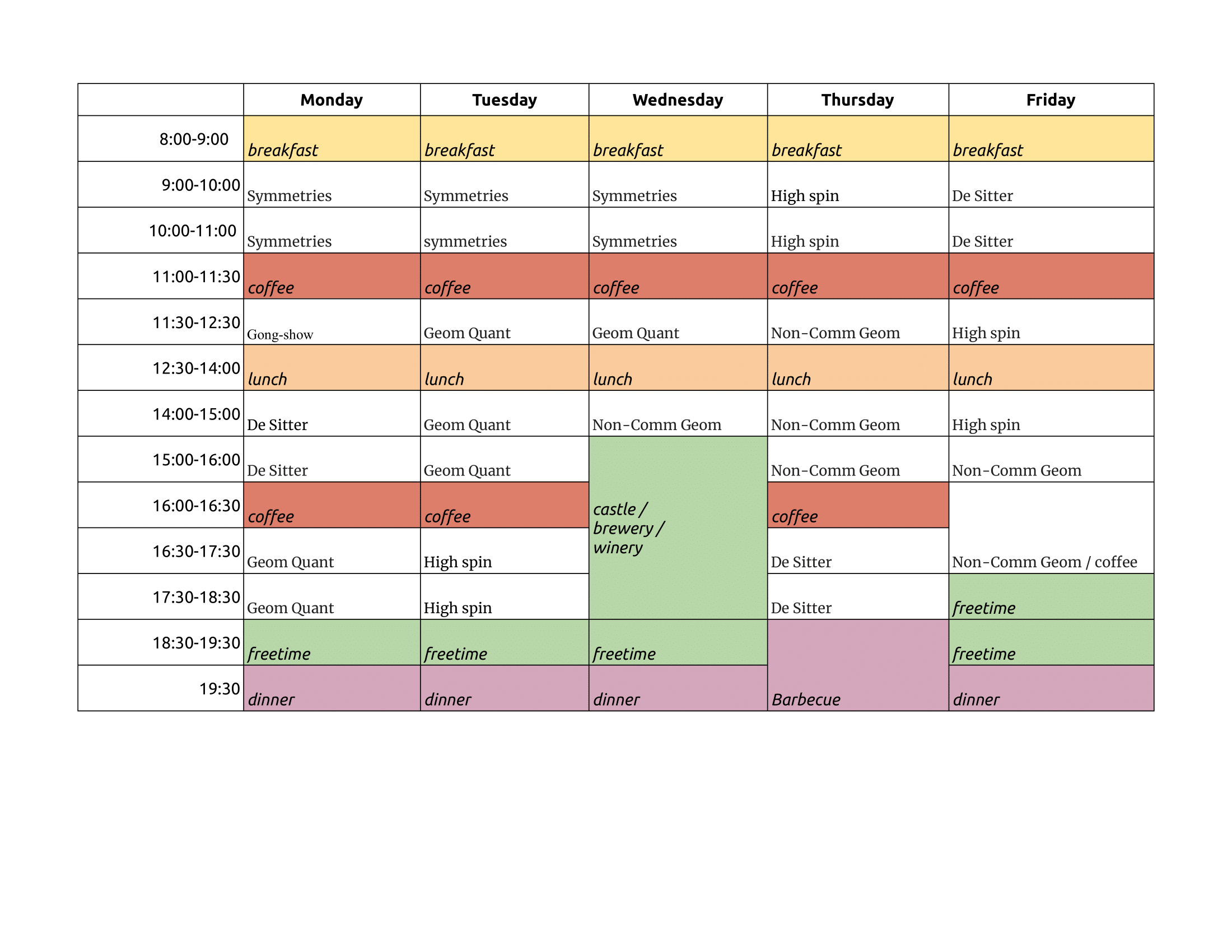
Schedule

Please find below the schedule of the school. To download a PDF version, please click here.